K-Nearest Neighbors from Scratch in Python
Posted on March 16 2017 in Machine Learning

The \(k\)-nearest neighbors algorithm is a simple, yet powerful machine learning technique used for classification and regression. The basic premise is to use closest known data points to make a prediction; for instance, if \(k = 3\), then we'd use 3 nearest neighbors of a point in the test set. In this post, I'm going to use kNN for classifying hand-written digits from 0 to 9 as shown in the picture above. Here's the pseudocode for classification:
- Choose the number of nearest neighbors i.e. \(k = 5\).
- For each data point in the test set:
- Calculate the distance from the point to each of \(k\) nearest neighbors in the training set.
- Use the majority class voting among \(k\) training points to assign the best class to the test point.
For regression, the algorithm takes the average of \(k\) training points instead of the majority class vote. It's important to be able to reimplement machine learning algorithms from scratch without using scikit-learn. Below is the Python script I've written that searches a sorted list in \(O(logK)\) which could be improved with a ball tree or a kd tree. The get_data() function retrieves the training MNIST dataset downloaded to my working directory, fit() function just stores the training data and class labels, and the predict() function does all the job of classifying the test labels. I choose the best \(k\) value that minimizes the misclassification error on a validation set. I use a repeated cross-validation here, running 10 repeats of 10-fold CV of the training set for each \(k\) from 1 to 19, but since the CV score of each repeat doesn't vary much, it should be fine to do a single 10-fold CV to increase computational efficiency. I also randomly take 3000 data points from the original training set and set aside \(1/3\) of them to be the test set since the original training set is quite large. I use the simple kNN algorithm here but there exist more robust kNN algorithms out there such as the Weighted kNN which weights each data point by its distance to the training point.
#!/usr/bin/python
import math
import numpy as np
import pandas as pd
from sortedcontainers import SortedList
from datetime import datetime
from random import randint, seed, random
def get_data(limit=None):
print 'Reading in and transforming data...'
df = pd.read_csv('train.csv')
data = df.as_matrix()
np.random.shuffle(data)
X = data[:, 1:] / 255.0
Y = data[:, 0]
if limit is not None:
X, Y = X[:limit], Y[:limit]
return X, Y
class KNN(object):
def __init__(self, k, classify):
self.k = k
self.classify = classify
def fit(self, X, y):
self.X = X
self.y = y
def predict(self, X):
y = np.zeros(len(X))
for i, x in enumerate(X):
sl = SortedList(load=self.k)
for j, xt in enumerate(self.X):
diff = x - xt
d = diff.dot(diff)
if len(sl) < self.k:
sl.add((d, self.y[j]))
else:
if d < sl[-1][0]:
del sl[-1]
sl.add((d, self.y[j]))
if self.classify == True:
votes = {}
for _, v in sl:
votes[v] = votes.get(v, 0) + 1
max_votes = 0
max_votes_class = -1
for v, count in votes.iteritems():
if count > max_votes:
max_votes = count
max_votes_class = v
y[i] = max_votes_class
else:
y[i] = np.mean([pred[1] for pred in sl])
return y
def score(self, X, Y):
P = self.predict(X)
if self.classify == True:
return np.mean(P != Y)
else:
return np.mean(math.pow(P - Y, 2))
if __name__=='__main__':
X, Y = get_data(3000)
Ntrain = 2000
Xtrain, Ytrain = X[:Ntrain], Y[:Ntrain]
Xtest, Ytest = X[Ntrain:], Y[Ntrain:]
t0 = datetime.now()
fold = 10
smoothness = 10
kcv_scores = []
for k in range(1, 20):
re_scores = []
for v in range(smoothness):
rlist = [[] for i in range(fold)]
for u in range(len(Xtrain)):
seed(u + v*16000000)
rlist[randint(0,9)].append(u)
r_fold_size = [len(a) for a in rlist]
R = sum(r_fold_size)
cv_scores = []
for w in range(len(rlist)):
xtrain = np.array([x for i, x in enumerate(Xtrain) if i not in rlist[w]])
ytrain = np.array([y for j, y in enumerate(Ytrain) if j not in rlist[w]])
xtest = Xtrain[rlist[w]]
ytest = Ytrain[rlist[w]]
knn = KNN(k, classify=True)
knn.fit(xtrain, ytrain)
cv_scores.append(knn.score(xtest, ytest))
avg_score = sum([a * b / R for a, b in zip(cv_scores, r_fold_size)])
re_scores.append(avg_score)
kcv_scores.append(np.mean(re_scores))
print 'Done with k =', k
print 'Repeated CV time:', (datetime.now() - t0)
k_optim = np.argmin(kcv_scores) + 1
print kcv_scores
print 'Min error:', min(kcv_scores)
print 'Optimal k:', k_optim
t0 = datetime.now()
knn = KNN(k=k_optim, classify=True)
knn.fit(Xtrain, Ytrain)
print 'Test error:', knn.score(Xtest, Ytest)
print 'Test time:', (datetime.now() - t0)
print 'Done!'
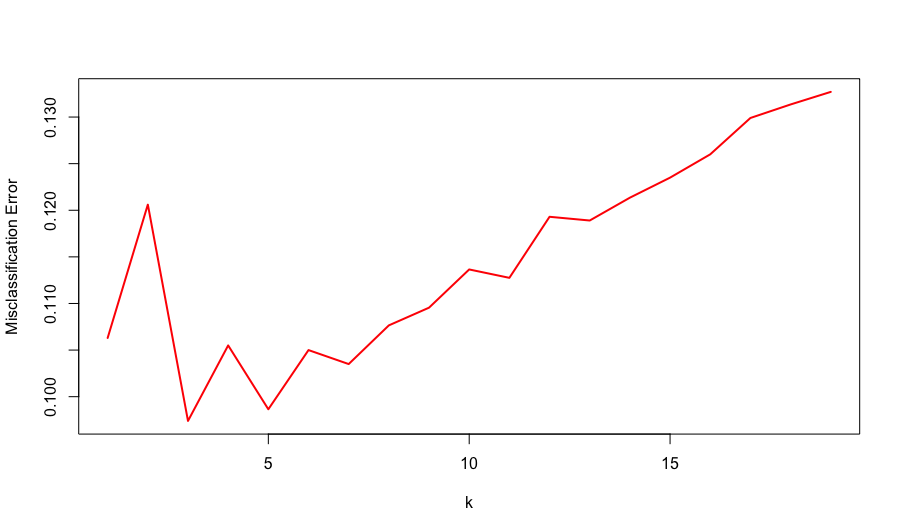
Here is the plot of misclassification error by \(k\) from repeated cross validation. The minimum validation error is 0.0974 achieved when \(k = 3\). Using this optimal value of \(k\), we'd fit a kNN on the entire training set and predict on the test set. The test error is 0.1 which is very close to the validation error we got for \(k = 3\). The model prediction takes about a minute. For more information about the mechanism of kNN, take a look at this blog post.